QR分解の定理・証明

この記事では、QR分解の式の証明ついて解説します。

QR分解とは
QR分解の定理（公式）
QR分解の証明

QR分解とは

QR分解とは、線形代数において行列を直交行列Qと、上三角行列Rの積に分解する手法です。
線型最小二乗問題や固有値問題を解く時に利用されます。
QR分解を計算する手法としては、ギブンス回転、ハウスホルダー変換、グラム・シュミット分解などがあります。

QR分解の定理（公式）

任意の正則行列Xは、次式のように分解できます。

(1) $\begin{eqnarray*} X =QR \end{eqnarray*}$

ここで、Qは直交行列、Rは上三角行列です。
これをQR分解といいます。

QR分解の証明

n次の正則行列をXとします。

(2) $\begin{eqnarray*} X = [x_1, x_2, \cdots, x_n] \end{eqnarray*}$

このとき、Xの列ベクトル $x_1, x_2, \cdots, x_n$ は、互いに線形独立となります。
よって、シュミットの直交化より、互いに直交する単位ベクトル $y_1, y_2, \cdots, y_n$ を生成できます。

(3) $\begin{eqnarray*} y_1 &=& \frac{x_1}{||x_1||} \\ y_2 &=& \frac{ x_2 - (y_1, x_2)y_1 }{||x_2 - (y_1, x_2)y_1 ||} \\ \vdots \\ y_n &=& \frac{x_n - (y_1, x_n)y_1 - (y_2, x_n)y_2 - \cdots - (y_{n-1}, x_n)y_{n-1} }{|| x_n - (y_1, x_n)y_1 - (y_2, x_n)y_2 - \cdots - (y_{n-1}, x_n)y_{n-1} ||} \end{eqnarray*}$

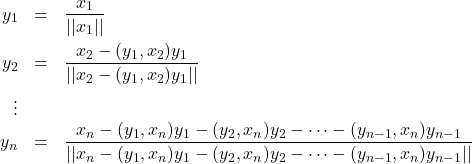
ここで、単位ベクトルは次式を満たします。

(4) $\begin{eqnarray*} (y_i, y_j) = \delta_{ij} \\ ( i,j=1,2,\cdots,n ) \end{eqnarray*}$

また、(1)式は

(5) $\begin{eqnarray*} x_1 &=& y_1||x_1 || \\ x_2 &=& y_1(y_1, x_2) + y_2 ||x_2 - (y_1, x_2)y_1 || \\ x_n &=& y_1(y_1, x_n) + y_2(y_2, x_n) + \cdots + y_{n-1}(y_{n-1}, x_n) + y_{n}|| x_n - (y_1, x_n)y_1 - \cdots - (y_{n-1}, x_n)y_{n-1} || \end{eqnarray*}$

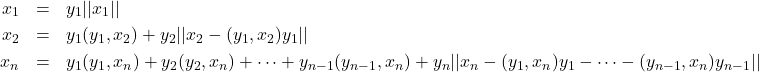
と書き直すことができ、これは行列の形で

(6) $\begin{eqnarray*} [x_1, x_2, \cdots, x_n] = \\ [y_1, y_2, \cdots, y_n] \left[ \begin{array}{cc} ||x_1 || & (y_1, x_2) & \cdots & (y_1, x_n) \\ 0 & ||x_2 - (y_1, x_2)y_1 ||& \cdots & (y_2, x_n) \\ 0 & 0& \ddots & \vdots \\ \vdots & \vdots & && \\ 0&0 & \cdots& || x_n - (y_1, x_n)y_1 - \cdots - (y_{n-1}, x_n)y_{n-1} || \end{array} \right] \end{eqnarray*}$

と整理できます。そしてQ, Rを

(7) $\begin{eqnarray*} Q &=& [y_1, y_2, \cdots, y_n] \\ \hspace{1mm} \\ R &=& \left[ \begin{array}{cc} ||x_1 || & (y_1, x_2) & \cdots & (y_1, x_n) \\ 0 & ||x_2 - (y_1, x_2)y_1 ||& \cdots & (y_2, x_n) \\ 0 & 0& \ddots & \vdots \\ \vdots & \vdots & && \\ 0&0 & \cdots& || x_n - (y_1, x_n)y_1 - \cdots - (y_{n-1}, x_n)y_{n-1} || \end{array} \right] \end{eqnarray*}$