k1sinθ+k2cosθ=k3の解を求める方法ついて紹介します。
k1sinθ+k2cosθ=k3の解の導出
【定理1】
(1) ![]()
の解は,つぎの式になります。
(2) ![]()
【証明】
(3) ![]()
より
(4) ![]()
(5) ![]()
ここで,![]() を求めることを考えます。 図より
を求めることを考えます。 図より
(6) ![]()
(7) ![]()
なので
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
また,![]() より
より
(12) ![]()
(13) 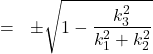
(14) 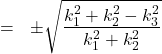
![]() が求まったので
が求まったので
(15) ![]()
![]() より分母を消去すると
より分母を消去すると
(16) ![]()
(17) ![]()
(証明終わり)
関連ページ

ロボット工学入門
ロボット工学の基本的なアルゴリズムや公式について入門者向けに解説します。

コメント