n軸周りの回転と変換行列の関係について紹介します。
n軸周りの回転行列
回転軸nまわりに角度θだけ回転させる変換行列はつぎのように表せます。
(1) 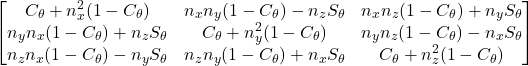
ここで,n=[nx, ny, nz]は単位ベクトルである.
例題
a=[1,1,0]を回転させ, b=[1,0,1]に一致させるための回転軸n(x軸以外)を1つ定め,その周り
の回転角度を計算してみます。
(解答1)
ベクトルa, bの外積cは
(2) 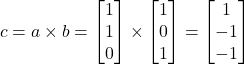
となる. ここで,cの単位ベクトルを回転軸nと定める.
(3) 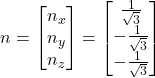
すると,(1)式より回転行列Aは
(4) 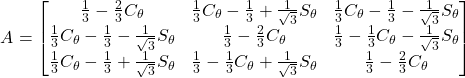
となる. ここで,b=A・aより
(5) 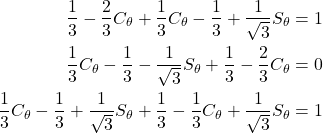
整理すると
(6) 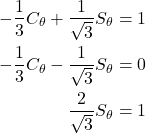
となり,求めたい回転角度θ=60となる.
<
回転行列(n軸周りの)から回転角の計算
n軸周りの回転行列Aが既知のとき,つぎの式から回転角θを求めることができる.
(7) ![]()
ただし,
(8) 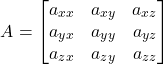
関連ページ
https://algorithm.joho.info/robotics-tutorial/


コメント