HoG SVM(識別器・分類器)による人検出のアルゴリズム・仕組み・計算方法についてまとめました。
【はじめに】HoG + SVMを組み合わせた識別器
HoG SVMは、物体検出に使われる識別器の1つです。
その名の通り、HoG特徴量とSVM(サポートベクタマシン)を組み合わせて識別器を作成します。
有名な画像処理ライブラリOpenCVにも実装されています。
人検出などに有効
顔検出の場合、どんな顔でも目や鼻、口の周囲の明暗差が大きく変わりません。
そのため、Haar-like特徴が有効でした。
しかし人間全身の場合、体の向きや服装の違いによって、明暗差は大きく変わります。
人検出では明暗差よりも輪郭情報を捉えたほうが検出精度が良いとされています。
そのため、人検出はHaar-like特徴よりもHoG特徴をよく使います。
【HoG特徴量とは】Histograms of Oriented Gradientsの概要
HoG(Histograms of Oriented Gradients)は、局所領域 (セル) の画素値の勾配方向ヒストグラム化したものです。
そのヒストグラムを特徴量としたのが、Hog特徴量です。
勾配を特徴量としているため、画像スケールに対してロバストであるという優れた特徴があります。
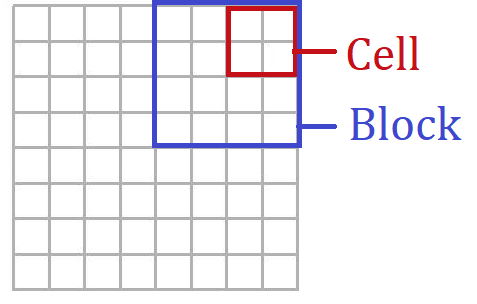
① 入力画像を複数のブロックに分割します。
また、各ブロックをセルに分割します。
■1ブロック(![]() セル)、1セル(
セル)、1セル(![]() ピクセル)で分割する場合
ピクセル)で分割する場合
② 入力画像![]() を微分します。
を微分します。
(1) ![]()
③ 微分画像から勾配強度![]() と勾配方向
と勾配方向![]() を求めます。
を求めます。
(2) 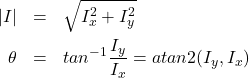
④ 勾配方向を9方向(0~180度まで20度ずつ)に量子化します。
⑤ セル毎に強度で重みを付けて勾配方向ヒストグラムを計算します。
⑥ ブロック毎に正規化し、特徴量を計算します。
(3) ![]()
![]() はn番目の勾配方向ヒストグラムです。
はn番目の勾配方向ヒストグラムです。
分母![]() は1ブロックのHOG特徴量の総和で次式で計算します。
は1ブロックのHOG特徴量の総和で次式で計算します。
(4) 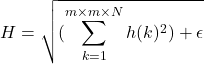
![]() はセルサイズ、
はセルサイズ、![]() は勾配方向数、
は勾配方向数、![]() です。
です。
⑦ 全てのヒストグラムを結合すればHoG特徴量の完成です。
【SVMとは】サポートベクターマシンの概要
サポートベクターマシン(通称:SVM)とは、高い汎化性能をもつ線形識別器の1つです。
2つのクラスがある2次元データ![]() がいくつかあるとします。
がいくつかあるとします。
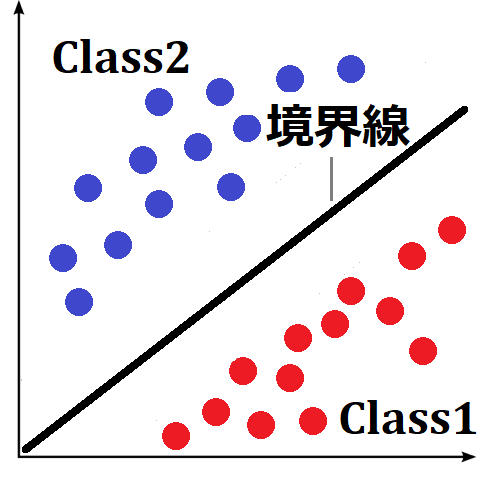
このとき、平面上に次式のような境界線(直線)を引くことで識別を行います。
(5) ![]()
SVMでは、いかに2つのクラスを綺麗に分ける境界線を引けるかが課題となります。
そのために、SVMでは「マージン最大化」というアイデアを用います。
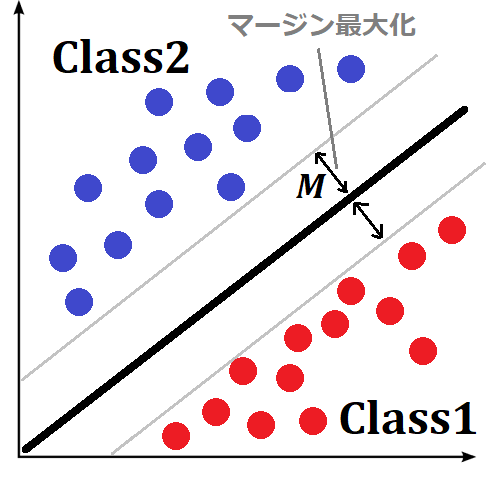
マージン最大化
マージンとは、「境界線」と「2つのクラス」間の距離![]() のことです。
のことです。
マージン最大化は、距離![]() が最大となるように境界線を決定することです。
が最大となるように境界線を決定することです。
距離が大きくなるほど、より多くの未学習データの判別が可能となります。(汎化能力の向上)


コメント