この記事では、Python+NumPyで単純パーセプトロンの重みを勾配降下法（最急降下法）で計算する方法をソースコード付きで紹介します。
単純パーセプトロンの重み算出（勾配降下法・最急降下法）
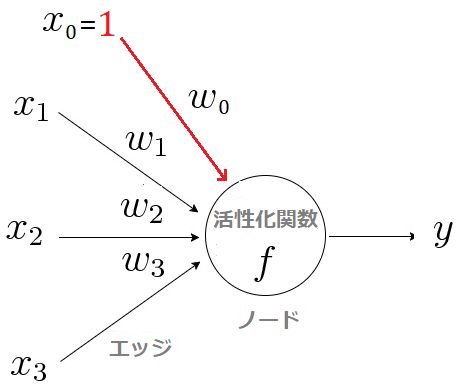
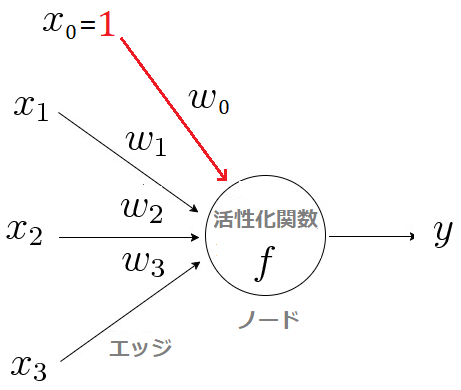
単純パーセプロトンとは、0番目の入力
を1、重み
を閾値とした場合のニューロンモデルのことです。
単純パーセプトロンの重みを最急降下法で計算した場合の手順は以下の通りです。
| – | 説明 |
|---|---|
| 1 | 初期パラメータ(学習率とエポック最大数)を設定します。 |
| 2 | 教師データ と正解ラベル のセットを用意します。 |
| 3 | 重み の初期値を適当に決めます。 |
| 4 | 教師データを単純パーセプトロンに入力します。 |
| 5 | 出力yと正解ラベルtを比較し、一致しなければ最急降下法で重みを更新します。 |
| 6 | 手順3～5をエポック最大数分だけ繰り返します。 |
ニューラルネットワークとは?基本原理と活性化関数、単純パーセプトロンについて徹底解説
ニューラルネットワークとは?基本原理と活性化関数、単純パーセプトロンについてまとめました。 ニューラルネットワークとは 脳内には、ニューロン（神経細胞）が無数にあります。ニューロン同士はシナプスで繋がっています。 入力される電気信号の電位が...
algorithm.joho.info
2017.12.21
単純パーセプトロンをPython + NumPyで実装してみましょう。
ソースコード（Python3）
サンプルプログラムのソースコードです。
教師データ
|
 |
 |
|
|---|---|---|---|
| 1 | 0 | 0 | -1(不正解) |
| 1 | 0 | 1 | -1(不正解) |
| 1 | 1 | 0 | -1(不正解) |
| 1 | 1 | 1 | 1(正解) |
AND演算（*）を学習させます。
はバイアス項なので全て1
【機械学習入門】アルゴリズム＆プログラミング
機械学習のアルゴリズム（原理）やプログラミング方法について入門者向けにまとめました。
algorithm.joho.info
2017.12.20
【Python超入門】使い方とサンプル集
Pythonとは、統計処理や機械学習、ディープラーニングといった数値計算分野を中心に幅広い用途で利用されている人気なプログラミング言語です。 主な特徴として「効率のよい、短くて読みやすいコードを書きやすい」、「ライブラリが豊富なのでサクッと...
algorithm.joho.info
2020.09.27
コメント