この記事では、物理学の斜面を転がる球の運動の計算式や例題について解説します。
## 斜面を転がる球の運動
下図のように斜面を転がっていく球の運動について考えます。

## 例題① 球が地面に到達する時間
【問題文】
球を傾斜角θの斜面上に置いて静かに放したあと、地面に到達するまでの時間Tを求めよ。
※球の質量m, 重力加速度の大きさg、球の地面からの高さh、球は質点とし、斜面との摩擦は無視する
【解答】
球が斜面上を運動中の加速度![]() は、斜面方向の運動方程式より
は、斜面方向の運動方程式より
(1) ![]()
となります。
また、地面に到達するまで斜面に沿って下降する距離Lは![]() なので、等加速度運動の公式より求めたい時間Tは
なので、等加速度運動の公式より求めたい時間Tは
(2) 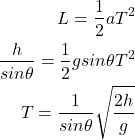
となります。
## 例題② 斜面角度を2倍にしたときの到達時間
【問題文】
例題①の斜面の角度を2倍にしたとき、地面への到達時間![]() は何倍になるか。
は何倍になるか。
【解答】
例題①の結果よりθを2θに置き換えると
(3) 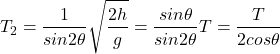
※![]()
よって、![]() 倍となる。
倍となる。

コメント
高校時代、数学を真面目に勉強しなかったので、サイン、コサインをほとんど憶えていません。したがって斜面を転がる球体が平面に達したときの速度の算出方法がこの式を見てもよくわかりません。
ただ、斜面の傾斜角度が大きくなると、速度は速くなりますよね。
中学校の理科で、転がり落ちた球体で平面に置いた木片を弾き飛ばして、その距離を測定する実験があります。この時、傾斜角を大きくしても、弾き飛ばされる距離は変わらないとあります。力学的エネルギー保存の法則がその理由です。
斜面の傾斜を大きくしても、球体を置く高さが同じであれば、斜面を転がる距離は短くなるので、平面に達した時の球体の速度は変わらないのでしょうか。そうであれば、木片を弾き飛ばすエネルギーを同じだと言えますよね。
どうなんでしょうか? ご指導ください。
運動量保存の法則で「同じ位置エネルギーが、同じように平面ですべて運動エネルギーに変換される」ので速度は変わらないと思います。
ちょっと自信なかったのでネットで調べると同じ質問をされている方と回答のページがありました。
https://noschool.asia/question/斜面の傾きを変えても落ちるスピードはなぜ同じ