2リンクマニピュレータの順運動学

ロボット

2016.10.22

2リンクマニピュレータの運動学計算式とその導出方法について紹介します。

## 順運動学の計算式 (2リンクマニピュレータ)

2リンクマニピュレータとは、2自由度のロボットアームのことです。
順運動学は、関節角度から手先位置を求めることです。
2リンクマニピュレータの順運動学の計算式は次のようになります。

(1) $\begin{eqnarray*} x=l_1cos\theta_1 + l_2cos(\theta_1+\theta_2)\\ y=l_1sin\theta_1 + l_2sin(\theta_1+\theta_2) \end{eqnarray*}$

ここで、 $x,y$ は手先位置、 $\theta_1, \theta_2$ は第１関節と第２関節のリンク角度、 $l_1, l_2$ は第1リンクと第２リンクの長さです。

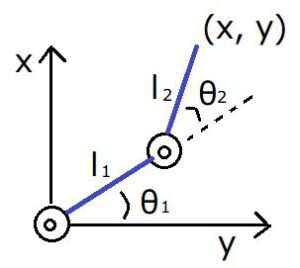
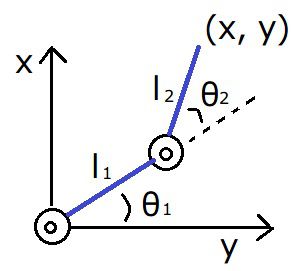
## 計算式の導出方法

マニピュレータの根元を原点(0 , 0)とします。
このとき、1つ目のリンク先の座標 $(x_1, y_1)$ は次のようになります。

(2) $\begin{eqnarray*} x_1=l_1cos\theta_1\\ y_1=l_1sin\theta_1 \end{eqnarray*}$

2つ目のリンク先の座標、つまり手先位置(x, y)は

(3) $\begin{eqnarray*} x=x_1 + l_2cos(\theta_1+\theta_2)\\ y=y_1 + l_2sin(\theta_1+\theta_2) \end{eqnarray*}$

となります。 $(x_1, y_1)$ は先程求めているので代入してやると

(4) $\begin{eqnarray*} x=l_1cos\theta_1 + l_2cos(\theta_1+\theta_2)\\ y=l_1sin\theta_1 + l_2sin(\theta_1+\theta_2) \end{eqnarray*}$

となります。順運動学の計算式は3リンク、4リンクも三角関数の定理を使うだけで求まります。