x-y-z軸周りの回転行列 (式・導出・証明・プログラム)

この記事では、x軸，y軸，z軸周りの回転行列を計算する公式と導出・証明・プログラムについて解説します。

x-y-z軸周りの回転行列
数値例
証明・導出
ソースコード
関連ページ

x-y-z軸周りの回転行列

x軸，y軸，z軸周りの回転行列をそれぞれRx(θ), Ry(θ), Rz(θ)とすると

(1) $\begin{equation*} R_x(\theta)=\begin{pmatrix}1 & 0 & 0 \\ 0 & C & -S \\ 0 & s & c \end{pmatrix} \end{equation*}$

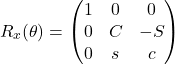
(2) $\begin{equation*} R_y(\theta)=\begin{pmatrix}C & 0 & -S \\ 0 & 1 & 0 \\ S & 0 & C \end{pmatrix} \end{equation*}$

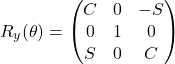
(3) $\begin{equation*} R_z(\theta)=\begin{pmatrix}C & -S & 0 \\ S & C & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}$

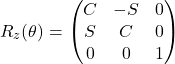
となります。
※ S = sinθ、C = cosθ として省略形で書いています

数値例

a=(1,1,0)をx軸まわりに90度回転させたベクトルbを求めます。
回転後のベクトルを求めるには、回転前のベクトルの左に回転行列をかければ良いので

(4) $\begin{equation*} b=R_x(90)・a=\begin{pmatrix}1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}・\begin{pmatrix}1 \\ 1 \\ 0 \end{pmatrix}=\begin{pmatrix}1 \\ 0 \\ 1 \end{pmatrix} \end{equation*}$

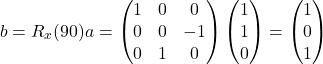
となります。

証明・導出

x軸周りの回転は下図のように表せます。
ここで，ex, ey, ezは単位ベクトルなので

(5) $\begin{equation*} e_x=1 \\ \end{equation*}$

(6) $\begin{equation*} e_y=C-S \\ \end{equation*}$

(7) $\begin{equation*} e_z=S-C \end{equation*}$

となります。
e=[ex, ey, ez]^Tとおくと

(8) $\begin{equation*} e=\begin{pmatrix}1 & 0 & 0 \\ 0 & C & -S \\ 0 & S & C \end{pmatrix}・\begin{pmatrix}1 \\ 1 \\ 1 \end{pmatrix} \end{equation*}$

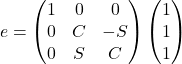
となります。
上式はベクトル[1, 1, 1]^Tをx軸周りにθだけ回転させたときベクトルeになることを示しています。
よってx軸周りの回転行列Rx(θ)は

(9) $\begin{equation*} R_x(\theta)=\begin{pmatrix}1 & 0 & 0 \\ 0 & C & -S \\ 0 & s & c \end{pmatrix} \end{equation*}$

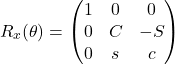
となります。
以後、同様に考えるとy軸, z軸周りの回転行列も求まります。

ソースコード

回転行列を計算するサンプルプログラムのソースコードは下記事で解説しています・
・【Python】回転行列の計算
・【C言語】回転行列の計算
・【Javascript】回転行列の計算

x-y-z軸周りの回転行列

数値例

証明・導出

ソースコード

関連ページ

コメント