モンテカルロ法とは?円周率を計算するあるアルゴリスムの例について入門者向けにまとめました。
## 【はじめに】モンテカルロ法とは
モンテカルロ法とは、乱数を用いてシミュレーションや数値計算を行う手法の1つです。
コンピューターで大量の乱数を生成し、条件式に当てはめていくことで短時間で近似解を求めていきます。
## 【円周率】モンテカルロ法で計算
モンテカルロ法の基本原理を理解するための有名な実用例として「円周率の近似値の計算」があります。
まずは計算手順を見てみましょう。
| 手順 | 操作内容 |
|---|---|
| ① | 正方形(1×1)内に点をランダムで生成します。 |
| ② | 「生成した点」と「原点」の距離が1以下なら1ポイント、1より大きいなら0ポイントを与えます。 |
| ③ | 手順①②の操作をN回繰り返し、合計ポイントPを計算します。 |
| ④ | 合計ポイントPを4倍し、試行回数Nで割った値が円周率(近似値)となります。 ( |
アルゴリズム解説
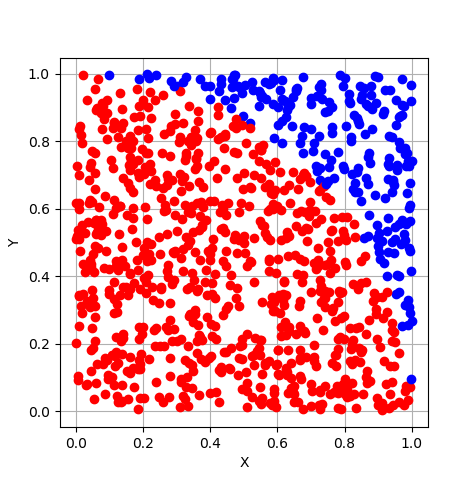
| 点種 | 意味 |
|---|---|
| 赤点 | 1/4分割された半径1の円内部 |
| 青点 | 1/4分割された半径1の円外部 |
合計ポイントPは、1/4分割された半径1の円内部にある点の個数(赤点の総数)を表しています。よって、![]() は、すべての点(青点と赤点)のうち、1/4分割された半径1の円の内部に入った点(赤点)の割合を表しています。
は、すべての点(青点と赤点)のうち、1/4分割された半径1の円の内部に入った点(赤点)の割合を表しています。
また、正方形の面積![]() 、1/4分割された半径1の円の面積
、1/4分割された半径1の円の面積![]() は次のようになります。
は次のようになります。
(1) 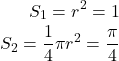
よって、円周率![]() は次式で計算できます。
は次式で計算できます。
(2) 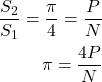
実装例
プログラミングでの実装例について下記事で紹介しています。
| – | 実装例 |
|---|---|
| 1 | ■【Python】モンテカルロ法の実装(円周率の計算) |
| – | 関連ページ・参考文献 |
|---|---|
| 関連記事 | ■【機械学習入門】アルゴリズム&プログラミング |

コメント
モンテカルロ法で円周率を計算するプログラムをswiftで作成する方法をしりたいです。