CNN(畳み込みニューラルネットワーク)の原理・仕組みについてまとめました。
畳み込みニューラルネットワーク(CNN)とは
畳み込みニューラルネットワーク(CNN:Convolutional Neural Network)とは、ディープラーニングの手法の1つで、主に画像認識に利用されています。
ニューラルネットワークの重み計算に「畳み込み演算(Convolution)」が用いられていることから、CNNと呼ばれています。
畳み込み演算は、画像処理の基本である「空間フィルタリング」でも用いられています。
CNNは主に次の3つの層から構成されます。
| 層の種類 | 概要 |
|---|---|
| 入力層(Input Layer) | 入力データを与える層。入力データが画像の場合、1入力に1画素を与える。(例えば32×32[px]のRGB画像なら入力の次元数は32×32×3=3072) |
| 畳み込み層(Convolutional Layer) | 入力データに対して畳み込み演算を行い、特徴量を取り出す層。 |
| プーリング層(Pooling Layer) | 特徴量を圧縮する層。(ロバスト性向上、過学習防止、計算コスト抑制のため) |
| 全結合層(Fully Connected Layer) | 取り出した特徴量から重み付き和を計算する層。 |
| 出力層 | 重み付き和から予測結果を出力する層。 |
畳み込み層
畳み込み演算とは、画像処理の代表例である「輪郭抽出」「ぼかし処理」などの「空間フィルタリング」で用いられている演算です。
CNNでも畳み込み層でこの演算が利用されており、「認識したい対象に応じて空間フィルタ(畳み込み層)のパラメータを自動で学習」させます。
また、CNNでは学習するフィルタを事前に複数用意します。
複数用意しておくことで、例えば「輪郭」「色」など複数の要素を扱うことができ、高精度な認識を行うことができます。
入力された画像データは、用意されたフィルタ処理の枚数だけ増えます。(例えばフィルタが3つなら画像も3枚に増える)
畳み込み演算
2次元の入力データ![]() に対して、フィルタ
に対して、フィルタ![]() を用いて畳み込み演算をする場合、計算式は以下のようになります。
を用いて畳み込み演算をする場合、計算式は以下のようになります。
(1) ![]()
畳み込み演算の例
先程の計算式の理解を深めるために、3×3の入力画像![]() と、2×2のフィルタ
と、2×2のフィルタ![]() を例に計算してみます。
を例に計算してみます。
(2) ![Rendered by QuickLaTeX.com \begin{eqnarray*} u= \left[ \begin{array}{ccccc} u(0, 0) & u(1, 0) & u(2, 0)\\ u(0, 1) & u(1, 1) & u(2, 1)\\ u(0, 2) & u(1, 2) & u(2, 2)\\ \end{array} \right], h= \left[ \begin{array}{ccccc} h(0, 0) & h(1, 0)\\ h(0, 1) & h(1, 1)\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-7c77d0acbe947a7e117d43ea0822592a_l3.png)
出力![]() は次のようになります。
は次のようになります。
(3) ![]()
![]() の各要素は次式で計算します。
の各要素は次式で計算します。
(4) 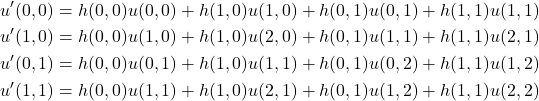
![]() は特徴マップと呼ばれ、元画像が
は特徴マップと呼ばれ、元画像が![]() のサイズに圧縮(簡略化)されたものです。
のサイズに圧縮(簡略化)されたものです。
入力が3次元の場合
RGB画像など、入力が3次元の場合はフィルタも3つ用意します。
そして、R、G、Bそれぞれに対してフィルタを1つ使って畳み込み演算します。
(5) 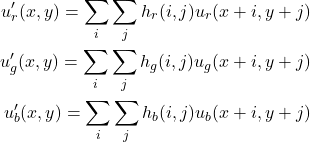
ゼロパディング処理
ゼロパディング処理とは、出力画像のサイズを調整する手法です。
やり方は単純で、入力データの周囲に0を外挿してやるだけです。
例えば、![]() の2次元の入力画像
の2次元の入力画像![]() に1[px]分だけゼロパディングしてやります。
に1[px]分だけゼロパディングしてやります。
(6) ![Rendered by QuickLaTeX.com \begin{eqnarray*} u= \left[ \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0\\ 0 & u(0, 0) & u(1, 0) & u(2, 0) & 0\\ 0 & u(0, 1) & u(1, 1) & u(2, 1) & 0\\ 0 & u(0, 2) & u(1, 2) & u(2, 2) & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{array} \right], h= \left[ \begin{array}{ccccc} h(0, 0) & h(1, 0)\\ h(0, 1) & h(1, 1)\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-721d9d5523946a6c712e3bff6dfef28f_l3.png)
ゼロパディング後の入力画像のサイズは![]() となり、サイズ
となり、サイズ![]() のフィルタ
のフィルタ![]() で畳み込み演算すると出力画像のサイズは
で畳み込み演算すると出力画像のサイズは![]() と大きくなります。
と大きくなります。
ストライド
ストライドも、ゼロパディング処理同様に出力画像のサイズを調整する手法です。
ストライドでは、畳み込み演算する際のフィルタの移動量を変化させることで、出力画像のサイズを変化させます。
上記の畳込み演算では、移動量1(ストライド1)でしたが、それを2にすると出力画像のサイズも小さくなります。
その分、情報量も失われます。
プーリング層(Pooling Layer)
プーリング層(Pooling Layer)は、は畳み込み層の後に利用されるのが一般的です。
この層では、入力データを圧縮(Down sampling)します。
圧縮することで以下のメリットが得られ、使い勝手が向上します。
| – | 圧縮するメリット |
|---|---|
| 1 | ロバスト性の向上(微小な位置変化の影響を受けにくくなる) |
| 2 | 過学習防止対策になる |
| 3 | 計算コストを抑えられるを下げる |
圧縮する方法はいくつかあります。
Max Pooling
Max poolingは、入力データ(配列)の小領域から最大値のみを取り出します。
このように情報を圧縮することで
例えば4×4の入力![]() をMax poolingで2×2に圧縮することを考えます。
をMax poolingで2×2に圧縮することを考えます。
圧縮データ![]() は次のようになります。
は次のようになります。
(7) ![Rendered by QuickLaTeX.com \begin{eqnarray*} u'= \left[ \begin{array}{ccccc} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ 13 & 14 & 15 & 16\\ \end{array} \right], u''= \left[ \begin{array}{ccccc} 6 & 8\\ 14 & 16\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-14de99d1a55029aa598ba8b4535a7b43_l3.png)
全結合層(Fully Connected Layer)
全結合層(Fully Connected層)は、多層パーセプトロン(MLP)と同様のものです。
CNNの場合、出力層の手前に置かれるのが一般的です。
この部分で最終的な識別を行います。
また、出力層のユニット数はクラス数(分類する数)と一致させる必要があります。
出力ユニットの値![]() の計算は、多層パーセプトロン(MLP)と同じです。
の計算は、多層パーセプトロン(MLP)と同じです。
それぞれの入力ユニットの値![]() と、接続の重み
と、接続の重み![]() を内積してバイアス
を内積してバイアス![]() を加えます。
を加えます。
(8) ![]()
となります。ここで![]() は活性化関数と呼ばれるものです。
は活性化関数と呼ばれるものです。
| – | 関連ページ・参考文献 |
|---|---|
| 1 | ■【機械学習入門】アルゴリズム&プログラミング |
| 2 | ■畳み込みニューラルネットワークの基礎 ■定番のConvolutional Neural Networkをゼロから理解する ■Convolutional Neural Networkとは何なのか ■畳み込みニューラルネットワークの構成 |


コメント