「SharpCap」でCMOSカメラ(SV305など)の映像が緑色になる件についてまとめました。
映像が緑色になる件
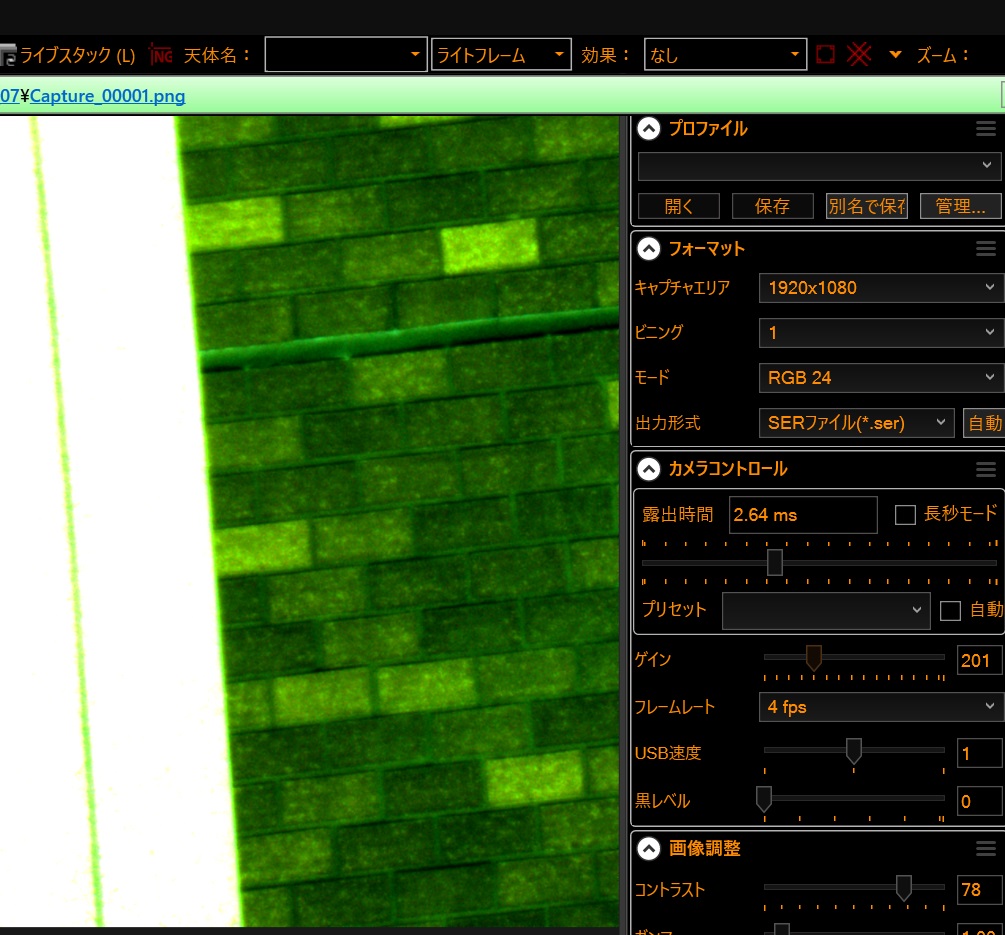
「SharpCap」でCMOSカメラ(SV305など)の映像が以下のように緑色になることがあります。
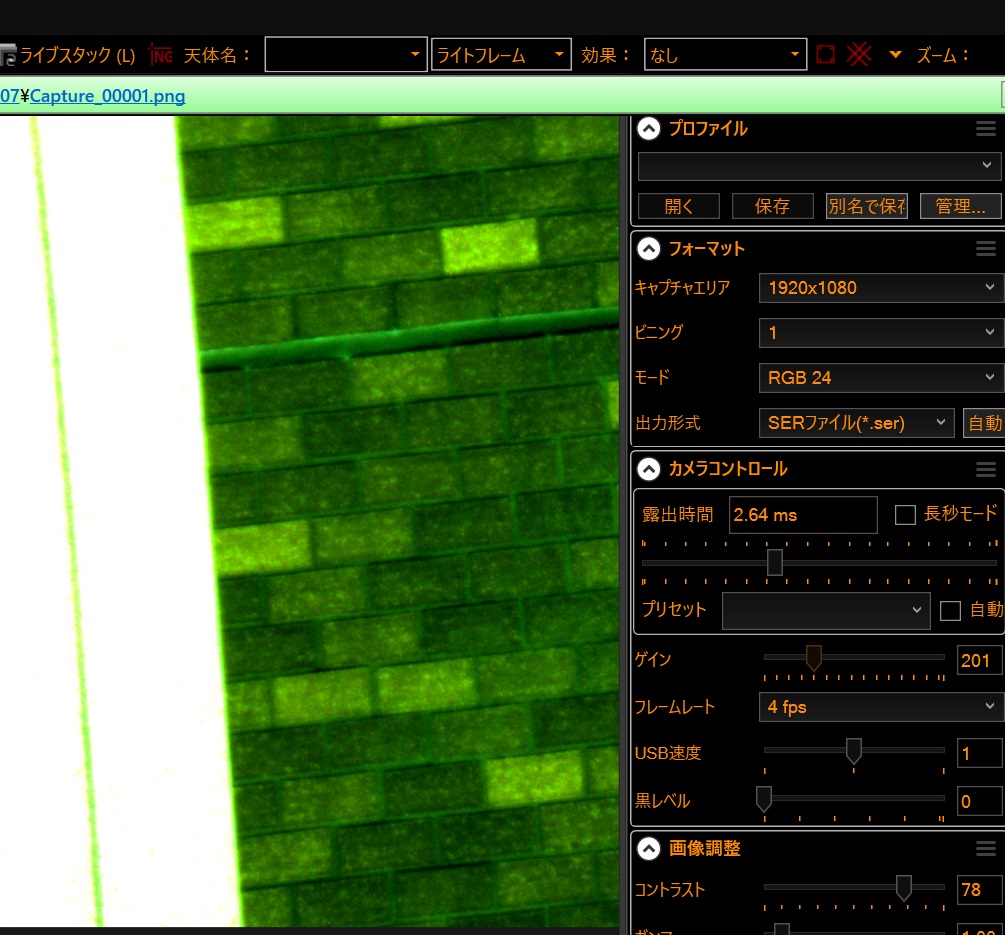
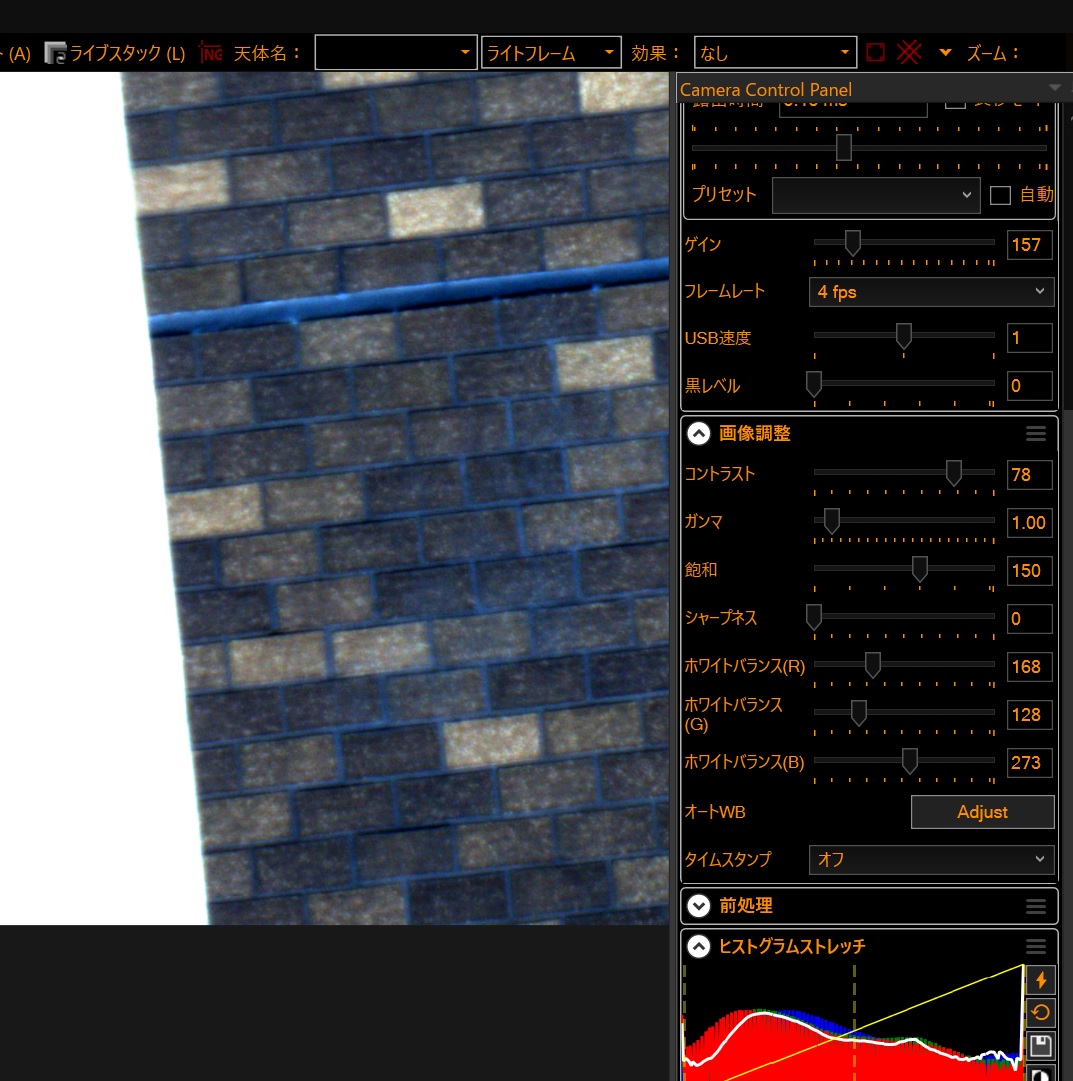
この場合、「画像調整(ImageControls)」「オートWB(AutoWhiteBalance)」にある「Ajast」を押すと、カラーバンスが調整されて解消されます。

【電視観望入門】格安望遠鏡+CMOSカメラ+自動導入経緯台で実現
格安望遠鏡+CMOSカメラ+自動導入経緯台で電視観望を実現する方法についてまとめました。

コメント