Pythonモジュール「NumPy」のPCAクラスで主成分分析を行い、各次元の寄与率を計算する方法についてソースコード付きでまとめました。
主成分分析(寄与率の計算)
Pythonモジュール「NumPy」のPCAクラスで主成分分析を行い、各次元の寄与率を求めてみます。
| – | 主成分分析の原理についてはこちら |
|---|---|
| – | ■【主成分分析の原理】固有値・寄与率の関係や例題 |
サンプルコード
サンプルプログラムのソースコードです。
# -*- coding:utf-8 -*-
from matplotlib import pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
def main():
# サンプル数
N = 100
# 乱数係数
d = 5
# 2次元データの生成
x = np.arange(N) + np.random.rand(N) * d
y = np.arange(N) + np.random.rand(N) * d
features = np.vstack([x, y])
# 主成分分析(主成分に変換)
pca = PCA()
pca.fit(features)
transformed = pca.fit_transform(features)
# 主成分の寄与率を出力
print(pca.explained_variance_ratio_)
# グラフプロット
plt.scatter(x, y) # 入力データをプロット
plt.scatter(transformed[:, 0], transformed[:, 1]) # 主成分をプロット
plt.xlabel('x, pc1')
plt.ylabel('y, pc2')
plt.grid()
plt.show()
if __name__ == '__main__':
main()
実行結果
サンプルプログラムの実行結果です。
寄与率の出力
[ 1.00000000e+00 1.01930579e-29]
グラフ
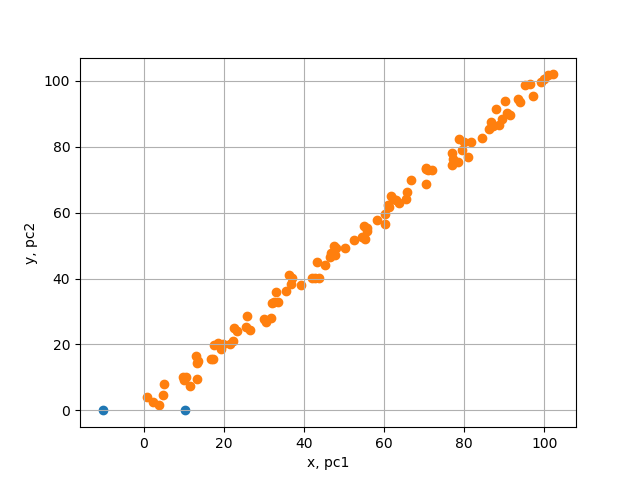
| – | 関連記事 |
|---|---|
| 1 | ■NumPy入門 サンプル集 |
| 2 | ■Python入門 基本文法 |

コメント