この記事では、CR回路(微分回路)の電流・電圧波形や計算式などの原理について解説します。
【微分回路】CR回路の計算式
入力信号(電圧)の時間微分(傾き)を出力する回路を微分回路といいます。
微分回路は、「パルスの検出」「ベースラインの除去」「ハイパスフィルター」「ビデオ信号の同期検出」などに用いられています。
この記事では、微分回路の1つである抵抗(R)とコンデンサ(C) を直列接続したCR回路の仕組みについて紹介します。
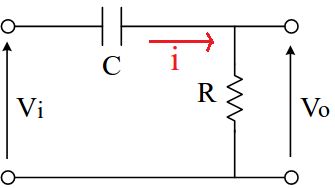
抵抗(R)とコンデンサ(C) を直列接続したCR回路は下図のようになります。
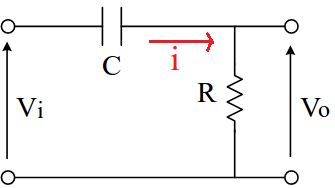
電圧/電流
入力電圧を![]() とするとき、時刻
とするとき、時刻![]() における出力電圧
における出力電圧![]() と電流
と電流![]() は次式で計算できます。
は次式で計算できます。
(1) 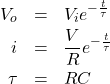
ここで、 ![]() は時定数と呼ばれ、回路の応答の速さを示しています。
は時定数と呼ばれ、回路の応答の速さを示しています。
時定数が大きいほど回路の応答が遅く、小さいほど応答が速いことを表します。
例えばパルス波(入力電圧)を加えた時の出力電圧の波形は下図のようになります
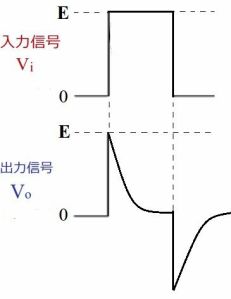
出力電圧の波形が入力電圧の波形を微分したような形になっていることがわかります。
時定数 ![]() が小さいほど応答が速くなるので、出力波形の傾きもより急勾配になります。
が小さいほど応答が速くなるので、出力波形の傾きもより急勾配になります。
時定数が小さいほど応答が速くなる理由
時定数が小さくなるほど応答が速くなる理由を計算式から考えていくと次のようになります。
| – | 考え方 |
|---|---|
| 1 | |
| 2 | |
| 3 | (※ |
| 4 | |
| 5 | 出力電圧の波形の傾きが急になる=応答が速い |
| 参考 | 【CR回路】時定数が小さいほど応答が速くなる理由 |
計算式の導出(証明)
先程の計算式を導きます。
抵抗(R)にかかる電圧(出力) ![]() 、コンデンサ(C)にかかる電圧
、コンデンサ(C)にかかる電圧 ![]() は
は
(2) 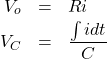
となります。よってキルヒホッフの法則より
(3) 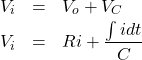
となります。次に両辺を ![]() で微分し、整理すると次式になります。
で微分し、整理すると次式になります。
(4) 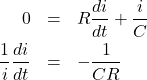
次に両辺を ![]() で積分し、整理すると次式になります。
で積分し、整理すると次式になります。
(5) 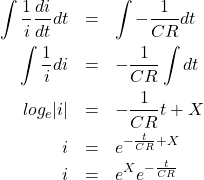
( ![]() は積分定数)
は積分定数)
ここで ![]() のときコンデンサは短絡状態となり、無視できるので
のときコンデンサは短絡状態となり、無視できるので ![]() となります。よってこれを上式に代入すると
となります。よってこれを上式に代入すると
(6) 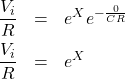
となり、未知数 ![]() が求まったのでCR回路を流れる電流
が求まったのでCR回路を流れる電流 ![]() は
は
(7) ![]()
となります。また、出力電圧 ![]() は
は
(8) ![]()
となります。(証明終わり)
| – | 関連記事 |
|---|---|
| 1 | 電気・電子回路入門 |
コメント