Pythonモジュール「NumPy」で数学関数、基本統計量を計算する方法についてまとめました。
## 【数学関数】指数関数、対数関数、円周率、ネイピア数e、ステップ関数、ランプ関数、シグモイド関数
指数関数、対数関数(底e、10、2) 、円周率、ネイピア数をNumPyで計算するサンプルです。
# -*- coding: utf-8 import numpy as np # 配列生成 x = np.array([1, 2, 3, 4, 5, 6]) # 指数関数の計算 y = np.exp(x) print(y) # 底eの対数関数loge(x) y = np.log(x) print(y) # 底10のlog10(x)の計算 y = np.log10(x) # 底2のlog2(x)の計算 y = np.log2(x) # ネイピア数e(自然対数の底) e = np.e print(e) # 2.718281828459045 # 円周率π pi = np.pi print(pi) # 3.141592653589793
| – | 関連記事 |
|---|---|
| 1 | ■【NumPy】指数関数の計算 |
| 2 | ■【NumPy】対数関数の計算 |
| 3 | ■【NumPy】底が10の対数関数 log10(x) |
| 4 | ■【NumPy】底が2の対数関数 log2(x) |
| 5 | ■【NumPy】円周率π、ネイピア数e |
三角関数
# -*- coding: utf-8 import numpy as np # xの値を生成(-3.14~3.14 0.25刻み) x = np.arange(-3.14, 3.14, 0.25) # sin関数の計算 y = np.sin(x) print(y) # sin関数の計算 y = np.cos(x) print(y) # tan関数の計算 y = np.tan(x) print(y)
| – | 関連記事 |
|---|---|
| 1 | ■【NumPy】正弦 numpy.sin(x) |
| 2 | ■【NumPy】余弦 numpy.cos(x) |
| 3 | ■【NumPy】正接 numpy.tan(x) |
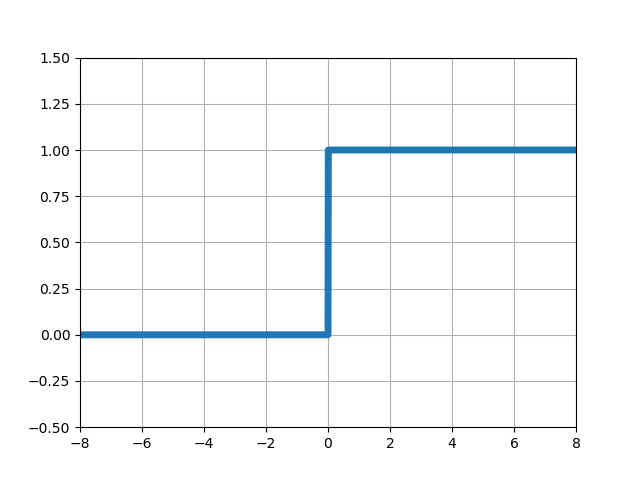
ステップ関数
ステップ関数は次の通りです。
(1) 
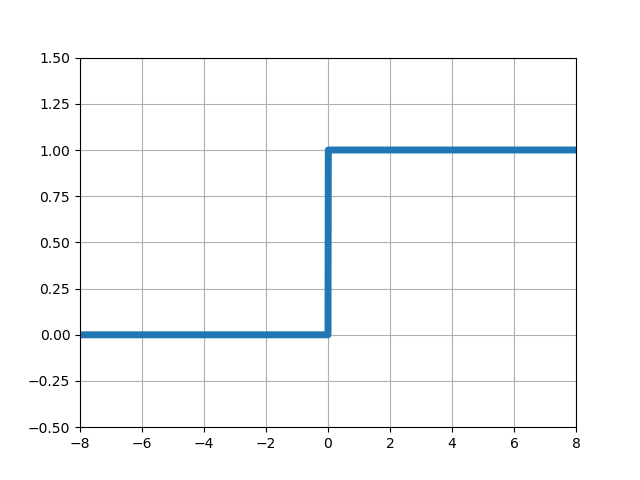
PythonとNumPy配列を使ってステップ関数を計算し、Matplotlibで計算結果をグラフに表示します。
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt # xの値(-8~8で0.1刻みで配列生成) x = np.arange(-8, 8, 0.01) # # ステップ関数 y = 1 * (x > 0) # グラフの設定 plt.plot(x, y, lw=5) # プロット plt.xlim(-8, 8) # x軸の範囲 plt.ylim(-0.5, 1.5) # y軸の範囲 plt.grid() # グリッド描画 plt.show() # グラフを出力
| – | 関連記事 |
|---|---|
| 1 | ■【NumPy/Matplotlib】ステップ関数(ヘビサイド・階段関数)のグラフ作成 |
ランプ関数(ReLU)
ランプ関数(ReLU)は次の通りです。
(2) ![]()
xが正の時はxをそのまま出力し、それ以外の時は0を出力します。
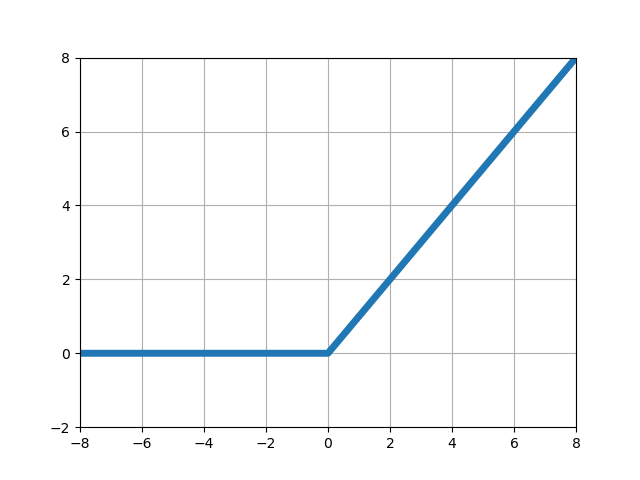
PythonとNumPy配列を使ってランプ関数(ReLU)を計算し、Matplotlibで計算結果をグラフに表示します。
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt # xの値(-8~8で0.1刻みで配列生成) x = np.arange(-8, 8, 0.1) # # ランプ関数 y = x * (x > 0) # グラフの設定 plt.plot(x, y, lw=5) # プロット plt.xlim(-8, 8) # x軸の範囲 plt.ylim(-2, 8) # y軸の範囲 plt.grid() # グリッド描画 plt.show() # グラフを出力
| – | 関連記事 |
|---|---|
| 1 | ■【NumPy/Matplotlib】ランプ関数(ReLU)のグラフ作成 |
シグモイド関数
シグモイド関数は次の通りです。
(3) ![]()
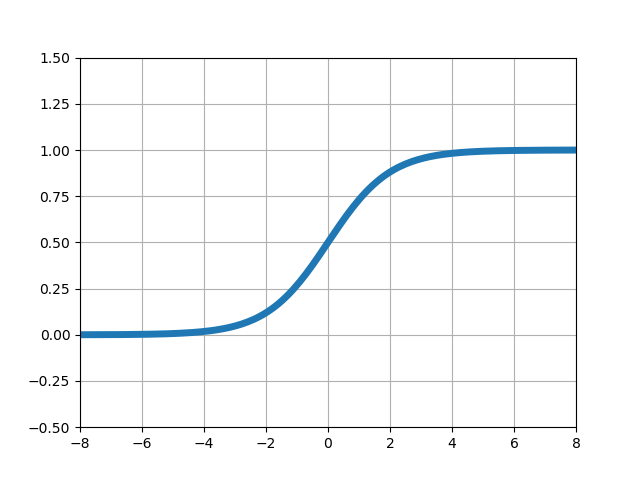
PythonとNumPy配列を使ってシグモイド関数を計算し、Matplotlibで計算結果をグラフに表示します。
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt # xの値(-8~8で0.1刻みで配列生成) x = np.arange(-8, 8, 0.1) # シグモイド関数 y = 1 / (1 + np.exp(-x) ) # グラフの設定 plt.plot(x, y) # プロット plt.xlim(-8, 8) # x軸の範囲 plt.ylim(-0.5, 1.5) # y軸の範囲 plt.grid() # グリッド描画 plt.show() # グラフを出力
| – | 関連記事 |
|---|---|
| 1 | ■【NumPy/Matplotlib】シグモイド関数のグラフ作成 |
## 【基本統計量】合計、平均、分散、標準偏差、不偏分散、不偏標準偏差、偏差値、最大値、最小値、中央値、算術平均、差分、勾配
# -*- coding: utf-8 -*-
import numpy as np
# データ
data = np.array([31,30,27,25,29,34,32,31,30,29])
# 合計を計算
sum = np.sum(data)
print("合計:", sum)
# 平均を計算
ave = np.average(data)
print("平均:", ave) # 結果を表示
# 分散を計算
var = np.var(data)
print("分散:", var) # 結果を表示
# 標準偏差を計算
std = np.std(data)
print("標準偏差:", std) # 結果を表示
# 不偏分散を計算
dvar = np.var(data, ddof=1)
print(dvar) # 5.76
# 不偏標準偏差を計算
dstd = np.std(data, ddof=1)
print(dstd)
# 偏差値を計算
ans = np.round_(50+10*(x-np.average(x))/np.std(x))
print(ans)
# 最大値を計算
max = np.amax(data)
print(max) # 34
# 最小値を計算
min = np.amin(data)
print(min) # 27
# 中央値を計算
median = np.median(data)
print(median) # 30.0
# 算術平均を計算
mean = np.mean(data)
print(mean) # 29.8
# xの差分を計算
diff_x = np.diff(x)
print(diff_x) #
| – | 詳細ページ |
|---|---|
| 詳細 | ■合計 ■平均 ■分散 ■標準偏差 ■不偏分散 ■不偏標準偏差 ■偏差値 ■最大値 ■最小値 ■中央値 ■算術平均 ■差分 ■勾配 |
【統計処理】点推定、区間推定、検定、回帰分析
| – | 詳細ページ |
|---|---|
| 詳細 | ■母平均の点推定 ■母分散の点推定 ■母比率の点推定 |
| 区間推定 | ■母平均の区間推定(t分布) ■母分散の区間推定(χ2分布) |
| 検定 | ■t検定 ■F検定 ■カイ二乗検定 |
| 回帰分析 | ■最小二乗法 ■重回帰分析 ■直線近似 ■曲線近似 ■株価予測 |
| – | 関連記事 |
|---|---|
| 1 | ■Python入門 サンプル集 |
| 2 | ■NumPy入門 サンプル集 |

コメント